Singular Value Decomposition

Singular Value Decomposition (SVD) is one of the core techniques of large scale data analysis and Data Science. If you have never heard of the SVD, but you know about linear regression, then it’s also worth knowning that SVD is at the heart of Linear Regression. When applied to text SVD is known as Latent Semantic Analysis.

If you want to know or to invest in one big-data tool that should be SVD because with it you can solve (semantic) search, prediction, dominant pattern extraction, clustering and topic modeling. That is why the SVD can be called the Swiss Army Knife of Big Data. I thought this is an original statement but it turns out others have beaten me to make this statement:

• Hacker News: “SVD is the swiss army knife of linear algebra - It’s a sledgehammer!! It breaks almost any problem you may encounter…”

• Sanjeev Arora: “A Swiss-army knife for provably solving various ‘clustering’ and ‘learning’ problems. (For reference, Sanjeev Arora is one of the top algorithms people today. He is currently a professor at Princeton and is a receiver of the Gödel and Fulkerson prizes.)

• Petros Drineas citing Diane O’Leary: “SVD is the Swiss Army knife of linear algebra” (For reference Petros Drineas is one of the top researchers in scalable linear algebra.)

Alternative (but not so fast) techniques

The SVD is one of the few techniques that scale really well. When I say scale I imagine something very concrete. I can convert Wikipedia to the so called latent semantic representation for about 30-60 minutes on a laptop computer with limited memory of 2-4GB. It depends how many passes one wants to do, but the whole process can be done in just three passes. However, if one wants more accuracy one can add more passes. For reference, just looping over the cleaned text of wikipedia while reading the data from disk takes about 5 minutes. The size of the Wikipedia text without formatting is 11GB. Another point of reference is that a more advanced software called Word2Vec (Google Word Vectors) is practically infeasbile with small resources (In my experience Word2Vec will crunch Wikipedia for a week; recently I heard the gensim implementation in Python is a lot faster).

Because of its scalability, output quality and wide applicability, the SVD is there to stay even though the technique dates back to the late 1800. The application of SVD to text, called Latent Semantic Analysis, is now 25 years old. The history of SVD is related to big names in mathematics and statistics like Jacobi, Beltrami, Jordan and Pearson.

Amazingly, the SVD connects core concepts in philosophy, language, mathematics, statistics, natural language processing, information retrieval and algorithms. In mathematics itself SVD is used in geometry, linear algebra and optimization. At the heart of SVD lies deep geometrical intuion, and it is no surprise SVD originated in geometry and not in algebra.

Nowadays, SVD can be employed to make money in e-commerce (recommendation systems), (semantic) search and web advertising. For example, Spotify uses SVD for music recommendations.

One curious trivia piece is that the original paper that proposed to use SVD for text search is called “A Solution to Plato’s Problem: The Latent Semantic Analysis Theory of Acquisition, Induction and Representation of Knowledge”. So there you go establishing a connection to 400 B.C. when Plato and Socrates were debating the nature of knowledge. But ok, what is the connection to the SVD?

Plato’s problem can be stated as “How do people connect the dots (or make inferences from limited knowledge)”? In the words of Chomsky who named this the “Plato’s problem” how is it that through limited experience or exposure to language people acquire advanced concepts they were never taught explicitly.

SVD: Connecting the dots

For example, through the use of SVD a computer can aquire lists containing country names or a list containing vegetable names.

query: germany
germany     1.0
italy       0.90
russia      0.89
sweden      0.88
spain       0.87
kingdom     0.87
france      0.86
republic    0.86
netherlands 0.86
poland      0.85

query: bulgaria
bulgaria    1.0
romania     0.91
croatia     0.89
hungary     0.88
slovakia    0.88
slovenia    0.87
serbia      0.87
macedonia   0.85
ukraine     0.84
albania     0.83

query: pepper
pepper      1.0
garlic      0.98
sauce       0.98
spices      0.97
onion       0.97
onions      0.97
fried       0.97
boiled      0.97
tomato      0.97
soup        0.97

Application of SVD may connect points such as “bulgaria” and “romania” that are two degrees of separation since there are many ways to reach any one from the other one. Connecting points two (or more) degrees of separation allows hidden connection to surface out.

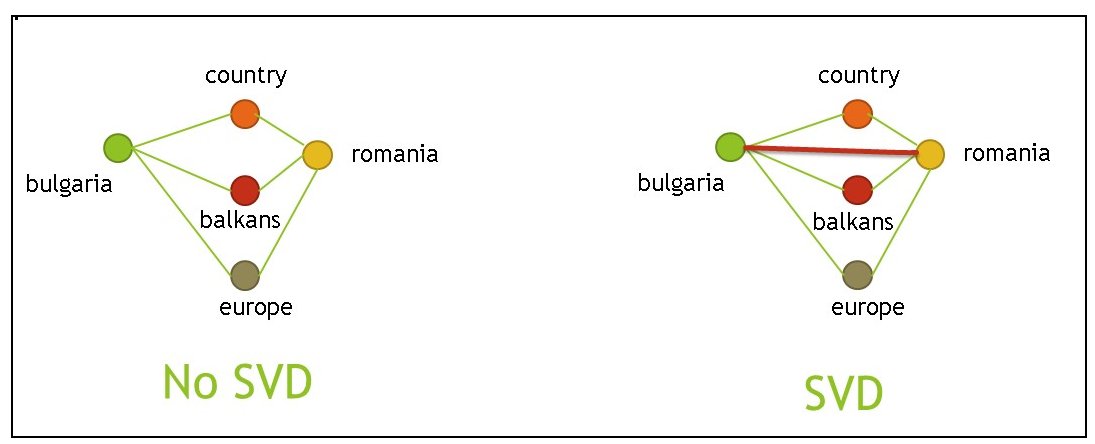
How does it actualy work

Follow Me to learn the tricks on how to compute the SVD on Wikipedia in 30 minutes (with approximations). Along the way, you’ll see other fascinating tricks related to scalable methods for high dimensional data. The methods have fancy names like random projections, hashing and sketching. There are also some simple but quite important tricks related to transforming word counts and modeling walks on graphs with matrix multiplication. I also explore the relationship between sparse co-occurence models and dense factorization models (when one is superior to the other - well they are complementary).

Planned Posts

• Very fast random projections
• Sketching techniques for co-occurence data
• Random walks on graphs and matrix multiplication
• When is sparse better than dense (or when simple co-occurence is better than factorization)
• When is it possible to search inside the data from matrix factorizations and when you should not
• The relationship between the hashing trick and SVD
• Local vs. global representations or how big to make the random walk on a graph
• Fitting SVD with or without gradient descent and what are the trade-offs