HyperLogLog Algorithm in Pictures - Algorithms for Big Data

Motivation

Suppose you want to count the number of unique visitors to your website. The obvious method is to create a hash set and add all the IP addresses to this structure. The size of the structure is the desired number of visitors. If the number of distinct visitors is too large the obvious approach will not work since the memory required to hold all unique IP addresses is too large. The HyperLogLog algorithm is the clever solution to this problem.

The HyperLogLog algorithm is an approximate probabilistic algorithm. Below I explain the intuition behind this algorithm using more pictures than actual math. This algorithm has been called magical since the obvious solution requires $n*\log(n)$ bits while the clever solution uses only $\log(\log(n))$ bits. I hope my explanation dispells some of the magic. It should be noted that the choice between the ‘obvious’ and the ‘clever’ algorithm entails a fundamental trade off between space and accuracy: if you compromise somewhat on the accuracy, you can save a lot of space.

Preliminaries

We can think of a long number as a bit string of 64 bits. One can map any string (or any object) to a long number or equivalently to a bit string by hashing. Well-chosen hash functions will ensure that distinct strings (objects) will produce distinct hashes in most cases. Even if the input consists of longs one should still hash them since it is essential that the algorithm operate on random bit strings. Hashing randomizes the actual ids. As we’ll see this randomization is very important.

Here is an encoding of some numbers as bit strings of 32 bits (the least significant bits are on the left side):

0 00000000000000000000000000000000
1 10000000000000000000000000000000
2 01000000000000000000000000000000
3 11000000000000000000000000000000
4 00100000000000000000000000000000
5 10100000000000000000000000000000
6 01100000000000000000000000000000

Here are some random numbers encoded as bit strings:

2989035304  00010100111100001001010001001101
2732191004  00111000101101111001101101000101
1704704513  10000000010111011101100110100110
1452012861  10111100101011111101000101101010
 741320636  00111101111001011111010000110100
1361178209  10000110011101111000010010001010
3435718421  10101000111001110001001100110011

Main intuition

Let’s organize the bit strings shown above into a binary tree as demonstrated on the picture below:

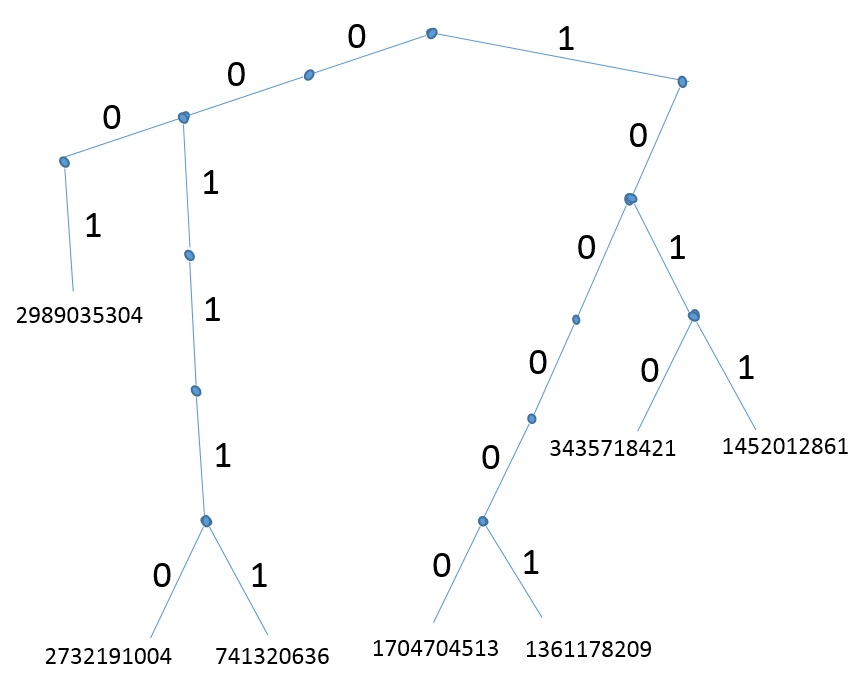
This drawing contains the main intuition behind the workings of the algorithm. Since the input is hashed to random bit strings, we can think as this process as building a tree from random strings. This means that we are essentially building a random tree. One can see that:

each branch is equally likely
each path to a leaf corresponds to a random input and is equally likely.

Since each leaf is equally likely the tree is balanced ignoring the variations that come from the randomness.

One fact to realize about balanced binary trees is that they are “extremely flat”. I mean the width of the tree is exponential in the hight as illustrated on the picture below:

If one has $n$ distinct items, they can be stored in a balanced binary tree of height $\log(n)$. To store the height itself, one needs $\log(height) = \log(\log(n))$ bits. When the tree is random, the height is a random variable with a value of around $\log(n)$. The HyperLogLog algorithm watches the height of the tree as we insert new items. Knowing the height, one can infer the size of the tree, which is related to the number of distinct items. The dynamics of the algorithm are illustrated in the following picture:

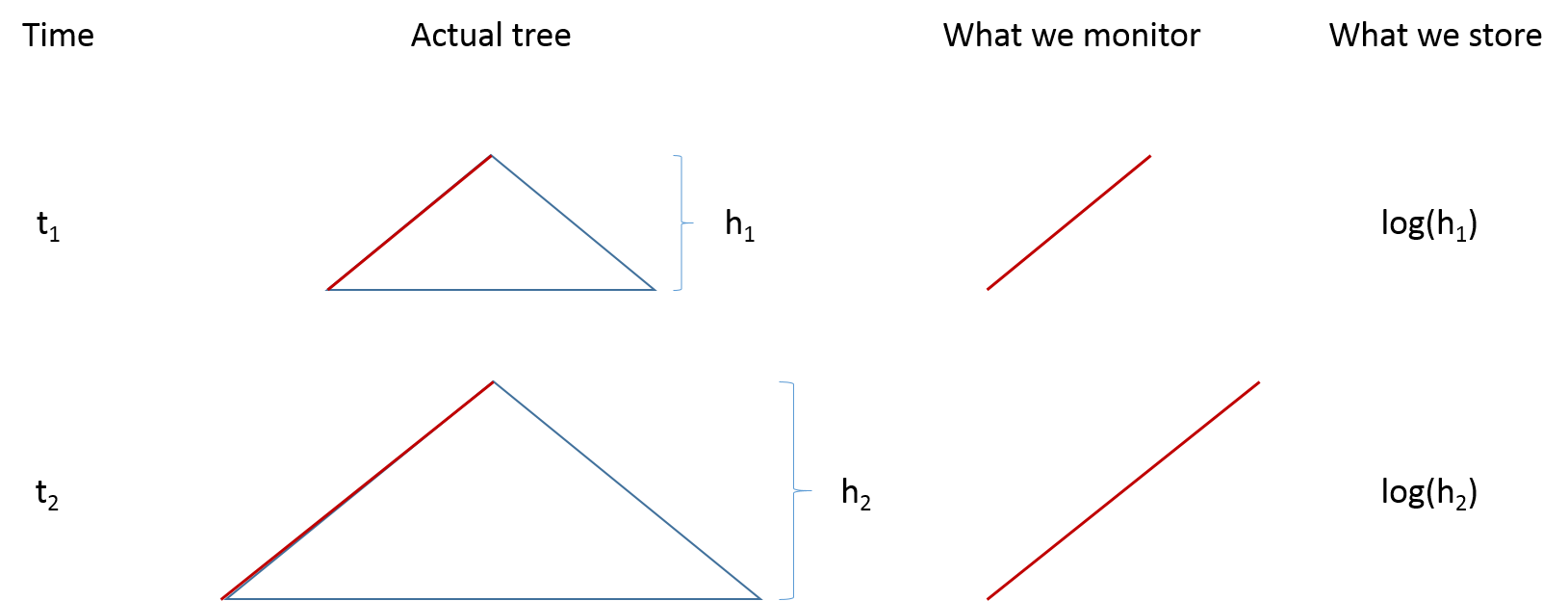
An important property of the algorithm is that seeing the same item again does not change the structure used for counting. This is because if an item is seen twice, it will simply re-generate the same path in the tree.

Main trick

The main trick is to get an estimate of the size of the tree without keeping the whole tree in memory. Since each path in the tree is equally likely, we can choose any path, for example 000…00, and put “sensors” on each possible branch. The branch on the chosen path which is deepest in the tree is indicative of the size of the tree.

Let’s choose the left-most path in the tree consisting entirely of 0’s. Let us keep looking at the path as new data comes in.

At first there is nothing on the path. So, the counter is set to 0.
Then suppose we observe 010… We increment the counter to 1.
If we see 10…, we do nothing. We ignore such inputs.
At some point we may see 001… Then we increment the counter to 2.
And so on.

As we see more and more data, we are likely to see longer strings with prefixes 00…01. For example, here is a simulation that shows how the prefixes of type 00…01 appear:

distinct number of prefixes skipped:             1 ['1011011000001011']
increment counter to  5 bits because of bit string: 0000011101010111
distinct number of prefixes skipped:    55 ['1011111111010100', '0111101000010010', ...]
increment counter to  6 bits because of bit string: 0000001011011101
distinct number of prefixes skipped:     59 ['0100011000011101', '0010000110101001', ...]
increment counter to  8 bits                        0000000011000101
distinct number of prefixes skipped:   117 ['0100011001010001', '1010011010101110', ...]
increment counter to  9 bits                        0000000001001001
distinct number of prefixes skipped:    179 ['1011100100111110', '0010001100010100', ...]
increment counter to 11 bits                        0000000000010001

As one can see the algorithm interleaves stages of skipping items that do not start with 00…01 (or start with 00..01 but were already seen) and increments a counter because of seeing a longer prefix of 00..01. If the counter is set to k at some stage, we expect to observe roughly 2^k distinct numbers before an increment of k happens. One can also observe that the counter is quite noisy. In the run above, the counter jumps directly to 5, skipping stages of 1,2,3, and 4.

Simple counting algorithm

let pattern = "00...0"
let counter = 0
on observing a new bit string:
   set counter = max(counter, longest_common_prefix(pattern, bit_string))
   set estimated_number_distinct_strings = from 2^(counter - 1) to 2^counter

The above procedure is a building block of the HyperLogLog algorithm.

Problems

As it was demonstrated above the counter is quite noisy. To reduce the variance of the estimate, multiple independent counters are used and averaged (or the median is taken).

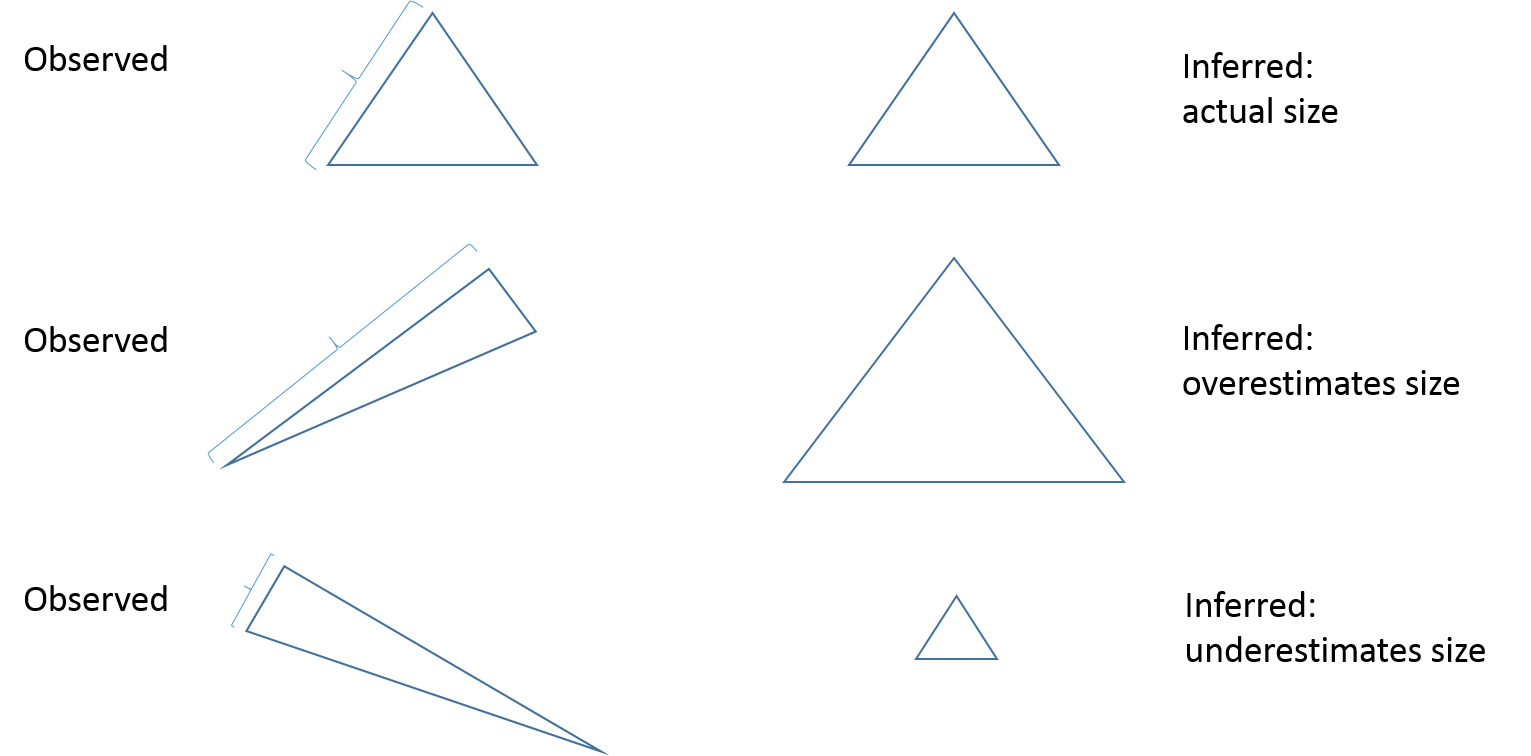
The picture below demonstrates some errors. The core of the method is to observe the left leg, but estimate the size of the whole tree. Due to variations we could observe a bigger left leg, but less full tree. In this case we will overestimate the size.

Implementations

widget counter code