How to be 40 Times Faster than the Obvious Approach
Executive Summary
I show on a real, practical problem that arises in search that one can write code that is 40 times faster than the obvious implementation in Java (Scala) (on the current benchmark).
The problem is related to running 10000 and more queries in batch mode which often arises.
The solution, I propose is based on modified Counting Sort and in practice can be used to compute 10000 queries in a few seconds. If such a solution is implemented in Elasticsearch, users will reap the benefit for batch queries.
Introduction
You have a few million pairs of keys and values and you wish to aggregate them, as in a group-by or a hash table. Of course, the hash table is the goto no-brainer solution, but this solution is quite slow.
What can you do when something is slow? In a typical solution architect style, you start asking about the requirements:
- what are the keys,
- how many of the keys are unique
- are the keys bounded in magnitude,
- are the values positive, and so on.
Requirements
For the problem I faced in my practice when implementing very fast algorithms for search and data mining, the following constraints were in place:
- the keys are bounded, e.g. from 0 to 10 million
- values are positive
- the counter is accessed many times so large pre-allocation or initialization time can be amortized
And if you are curious, the actual problem was to compute the search results for 10000 and more queries. As you can image for this requirement off-the shelf solution like Elasticsearch won’t work, unless they implement a batch queries functionality. However, the current algorithm can easily extend Elasticsearch with another endpoint called api/batchQueries and finish in seconds (on an in-memory index).
The Interface
The interface is simple:
- adding keys and values (e.g. in a loop)
- obtaining a summary at the end
trait Counter{
def add(key: Int, value: Int): Unit
def getCounts(): (Array[Int], Array[Int])
def getSortedCounts(top: Int): (Array[Int], Array[Int])
def reset(): Unit
}Naive Solution
The naive solution uses a HashMap (scala.mutable.HashMap). For ease of use, we can use a HashMap with default value. Thus, the core operation is simply map(key) += value.
object NaiveCounter{
def newMap(): mutable.Map[Int, Int] = {
mutable.HashMap[Int, Int]().withDefaultValue(0)
}
}
final class NaiveCounter extends Counter {
var map = NaiveCounter.newMap()
def add(key: Int, value: Int) = {
assert(value > 0)
map(key) += value
assert(map(key) > 0) // because we can overflow, and go to negative
}
def getCounts(): (Array[Int], Array[Int]) = {
map.toArray.unzip
}
def getSortedCounts(top: Int): (Array[Int], Array[Int]) = {
map.toArray.sortBy{case (key, value) => (-value, value)}.
take(top).unzip
}
def reset(): Unit = {
map = NaiveCounter.newMap()
}
}The above takes about 5-10 minutes to code. Easy, but slow, kills the garbage collector and will eventually run out of memory on trivial data sizes.
The Efficient Solution
The efficient solution makes use of the fact that the keys are bounded from 0 to some max integer (max_key). We will pre-allocate an array of counts initialized to zero from 0 to (max_key + 1). This allocation will cost time, so we need to use this solution many times to amortize the allocation time.
final class EfficientCounter(maxKey: Int) extends Counter {
val uniqueKeys = Array.ofDim[Int](maxKey + 1)
val counts = Array.ofDim[Int](maxKey + 1)
var nextFreeIdx = 0 // next free index in unique keys
var resultKeys: Array[Int] = null
var resultValues: Array[Int] = null
def add(key: Int, value: Int) = {
assert(value > 0)
assert(key <= maxKey)
if (counts(key) == 0){
uniqueKeys(nextFreeIdx) = key
nextFreeIdx += 1
}
counts(key) += value
assert(counts(key) > 0) // because we can overflow, and go to negative
}
def computeCountsAndReset(): (Array[Int], Array[Int]) = {
if (resultKeys == null) {
assert(resultValues == null)
val keys = Array.ofDim[Int](nextFreeIdx)
val values = Array.ofDim[Int](nextFreeIdx)
var i = 0
while (i < nextFreeIdx) {
val key = uniqueKeys(i)
val value = counts(key)
keys(i) = key
values(i) = value
counts(key) = 0 // reset
i += 1
}
nextFreeIdx = 0 // reset
resultKeys = keys // cache precomputed
resultValues = values
}
(resultKeys, resultValues)
}
def getCounts(): (Array[Int], Array[Int]) = {
computeCountsAndReset()
}
def getSortedCounts(top: Int): (Array[Int], Array[Int]) = {
val (keys, values) = getCounts()
keys.zip(values).sortBy{case (key, value) => (-value, key)}.
take(top).unzip
}
def reset(): Unit = {
resultKeys = null
resultValues = null
}
}As you can see the solution is more complicated but still reasonable. It makes use of two arrays of a size say a million. A million unique keys is a practical limit for many problems. The overhead is in this case 8 MBs.
Testing The Solution
I want to test the efficiency of the proposed solution, but what if, I have implemented incorrectly. Then my test is meaningless. More over, one should test independent of whether one cares for efficiency. Correcness comes first, then efficiency.
Test Strategy
There are multiple test stragies. For the purpose of this blogpost I implemented tests on randomly generated data. I made a VerifyingCounter class which applies the operations both on the naive and efficient implementation. When I retrieve the result counts, I want to make sure that both the naive implementation and the efficient implementation are the same.
There are other test strategies, and they should be implemented, but I only implemented this one, since I intend to reuse the same setup in benchmarking.
class VerifyingCounter(expected: Counter, observed: Counter,
assertFunc: (Boolean, String) => Unit) extends Counter {
def add(key: Int, value: Int): Unit = {
expected.add(key, value)
observed.add(key, value)
}
def getAsMap(counter: Counter): mutable.Map[Int, Int] = {
val (keys, values) = counter.getCounts()
val map = mutable.HashMap[Int, Int]()
for((k,v) <- keys.zip(values)){
map(k) = v
}
map
}
def getCounts(): (Array[Int], Array[Int]) = {
val expectedMap = getAsMap(expected)
val observedMap = getAsMap(observed)
assertFunc(expectedMap.equals(observedMap),
"Expected getCounts != observed getCounts")
(Array.empty, Array.empty) // return dummy, we don't care
}
def getSortedCounts(top: Int): (Array[Int], Array[Int]) = {
assertFunc(false, "getSortedCounts is not implemented")
throw new NotImplementedError()
}
def reset(): Unit = {
expected.reset()
observed.reset()
}
}And the acual test code:
class TestCounter extends FunSpec {
describe("TestCounter") {
it("small test") {
val rnd = new Random(4848488)
val initMaxID = 1000000
val verifyingCounter = new VerifyingCounter(new NaiveCounter(),
new EfficientCounter(initMaxID), (cond, desc) => {
assert(cond, desc)
})
for(i <- 0 to 10){
val (maxID, keys, values) = Generator.generateKeyValues(rnd, 1, 10, 1, 2)
assert(maxID <= initMaxID)
keys.zip(values).foreach{ case (key, value) => {
println(s"${key}: ${value}")
verifyingCounter.add(key, value)
}}
verifyingCounter.getCounts()
verifyingCounter.reset()
}
}
}
}Benchmarking
For benchmarking, I use the following code:
Generator
object Generator{
def generateKeyValues(rnd: Random,
uniqueFrequent: Int,
cntFrequent: Int,
uniqueInfrequent: Int,
cntInfrequent: Int): (Int, Array[Int], Array[Int]) = {
val maxID = uniqueFrequent + uniqueInfrequent
val c1 = cntFrequent*uniqueFrequent
val c2 = cntInfrequent*uniqueInfrequent
val pFreq = c1.toDouble/(c1 + c2)
val (keys, values) = Iterator.range(0, c1 + c2).map(_ => {
val p = rnd.nextDouble()
val id = if (p < pFreq){
rnd.nextInt(uniqueFrequent)
}
else{
uniqueFrequent + rnd.nextInt(uniqueInfrequent)
}
(id, 1)
}).toArray.unzip
(maxID, keys, values)
}
}Applying the Generator
class TestCounter extends FunSpec {
describe("TestCounter") {
it("benchmark"){
val rnd = new Random(4848488)
val initMaxID = 1000000
val uniqueFrequent = 1000
val cntFrequent = 2000
val uniqueInfrequent = 100000
val cntInfrequent = 1
val samples = List.range(0, 5).map(_=> {
val (maxID, keys, values) = Generator.generateKeyValues(rnd,
uniqueFrequent,
cntFrequent,
uniqueInfrequent,
cntInfrequent)
assert(maxID <= initMaxID)
(keys, values)
})
def timed(counter: Counter, name: String): Unit = {
Timer.timed(name, {
Range(0, 40).foreach(_ => {
for ((keys, values) <- samples) {
// we want to avoid unboxing
var i = 0
while (i < keys.length) {
counter.add(keys(i), values(i))
i += 1
}
counter.getCounts()
counter.reset()
}
})
})
}
// run only one and both sequentially
timed(new NaiveCounter(), "naive")
timed(new EfficientCounter(initMaxID), "efficient")
}
}Profiling
Profiling via jvisualvm shows that the bottleneck is computeCountsAndReset.
Results and Conclusion
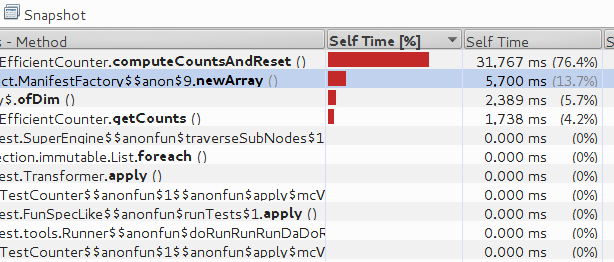
The results are below:
Time for 'naive' 39.005 secs. if run before the naive implementation
Time for 'naive' 36.308 secs. if run separate
Time for 'efficient' 1.682 secs. if run right after the naive implementation
Time for 'efficient' 806 ms. if run separatelyOne one can see the efficient implementation is more than 40 times faster when run alone. It is also the case that the naive implementation garbage collection is left to run after the naive implementation is finished and it affects other unrelated code.
The conclusion is that:
- Algorithms tuned to the specific requirements are beneficial
- Avoiding garbage collection is worth it
- Avoiding boxing/unboxing is worth it
- The scala and also java hash tables are not performant, partly because of garbage collection
Caveats
There are many things that affect code speed in addition to the algorithm used:
- data alignment
- reads/writes and cpu cache trashes
- cpu architectures and compiler
Additionally, algorithms are sensitive to the data distribution. For example, in a problem to find duplicates, sorting will win over hashing on nearly sorted arrays, but will lose if the array is shuffled randomly.